結合状態の規則性で重要なものに「互換性」があります。
　組織図の4大原則のうち
①結合状態を含めあすび通しを変更しても組織は変わらない
②結合状態を含め踏み木の踏み順を変更しても組織は変わらない
の2つから、一定の条件を満たす結合状態は相互に変換することができます。
　図1の6つの結合状態から作り出される結合状態は図2のように360（＝6*5*4*3））通りある事は前にもお話しました。

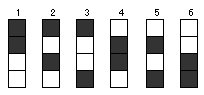
図1

図2

　今、図1の結合状態の中より、「対称」「反転」の視点から、図3のようなお互いに補完関係にあるペアーで構成される結合状態を選択すると、図4の72通り（＝3*4*3*2）の結合状態がある事が判ります。

図3

図4

　この72通りの結合状態は、最初にお話した2つの原則から、お互いにどのパターンへも変換が可能です。　図4の「1」の結合状態を最左列の「13,25,37,49,61」の結合状態に変換したものが図5です。

図5

1→25→49：あすび通しを変更（踏み木の踏み順は変更なし）
13→37→61：あすび通しを変更（踏み木の踏み順は変更なし）
1→13 ：踏み木の踏み順を変更（あすび通しは変更なし）
25→37 ：踏み木の踏み順を変更（あすび通しは変更なし）
49→61 ：踏み木の踏み順を変更（あすび通しは変更なし）

1から37,61に変換するには「踏み木の踏み順の変更」と「あすび通しの変更」が必要です。
72種類の結合状態が全て相互に互換性を持ちますから、1つの組織は72の組織図を持つという事になります。一見異なる組織図のように見えても、繰り返されている部位を整理し、結合状態を統一すると同一の組織となることは度々経験します。
　この「互換性」は、組織図を理解してゆく上で大変重要なkeyとなります。感覚的に一寸理解し難いものがありますが、組織図をたくさん書いてゆくと自然と納得ができるようになります。