対称性と繰返しは、柄の重要な基本的な要件の一つです。ここではその「対称性と繰返し」について考えてみます。
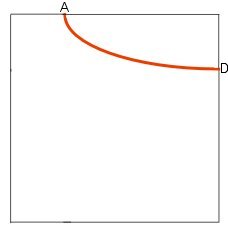
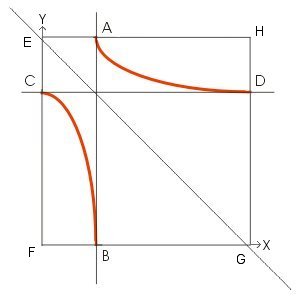
図1の曲線AD（辺EHから始まり辺HGで終る）から図2のような曲線BC（辺EFから始まり辺FGで終る）をつくります。曲線ADと曲線CBは次のような関係にあります。
対角線EGを対称軸とするため
1.曲線ADのAのx軸座標と曲線CBのBのX軸座標は同一
2.曲線ADのDのY軸座標と曲線CBのCのY軸座標は同一
また(AH=CF）>（AE=EC） （AH=CF）＝（AE=EC）の時は「円」または「矩形」

　図2でつくられた曲線を上下左右繰り返すと、図3のように交差しない連続した曲線が作り出されます。

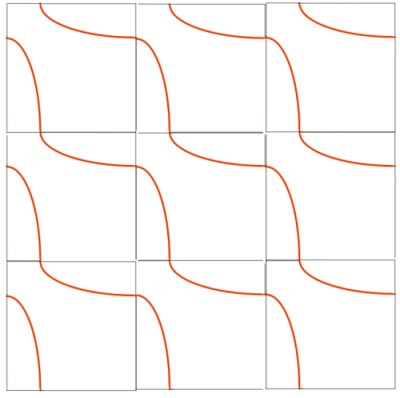
図3

　図2に沿ってこれを組織図で表現して見ます。(赤くペーストした部位は線を明確化するためのもので組織とは無関係です)

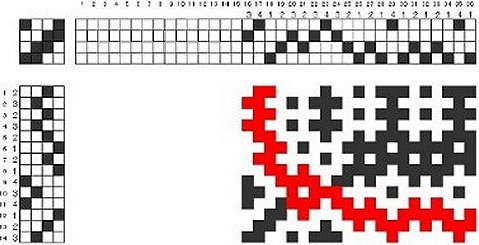
図4

　図4の組織に上記の3つの要件を加えたものが図5です。

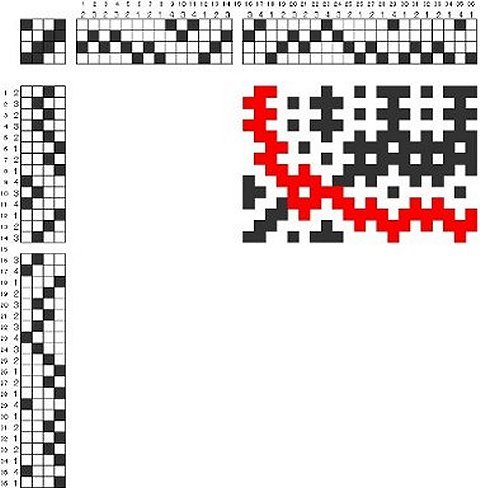
図5

　組織図を完成させたものが図6、図7は図6を展開したものです。

図6

図7

　柄としては未完成ですが取り敢えず交叉しない連続した曲線をつくる事ができました。
当然の事ですが、織りに現われる曲線は組織図の4大原則に基づき組織図に表現する事が可能です。様々な織りの状態を4大原則に沿って組織図に描いてみると、屑になった糸が解きほぐれる様に、整然と果てしなく拡がる手織りの世界が見えてきます。

柄として完成した例を図8に示しました。45°方向に連続した曲線を表現している事をお判り戴けると思います。

図8