柄の規則性のうち、「柄の規則性 対称」では「対称」の関係についてみましたが、ここでは「（裏表）反転」についてみてみます。図1は上下・左右とも（裏表）反転して柄が構成されています。

図1

　一般に「結合状態」の行列が図2のように補完関係にあるグループから構成されている場合は、同一の「結合状態」で「あすび通し」と「踏み木の踏み順」を変更することで、柄を反転することができます。これは「結合状態を含んであすび通し、踏み木の踏み順を変えても柄は変わらない」という組織図の2大原則にもとづきます。

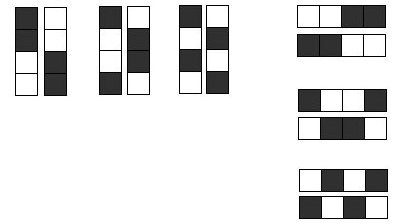
図2

図3でこの事を組織図にしてみます。

図3

Ⅱ：これを元図とします
Ⅰ：Ⅱを反転したものです。図1の補完関係の結合状態にあすび通しが変化しています。
Ⅲ：Ⅱを反転したものです。図1の補完関係の結合状態に踏み木の踏み順が変化しています。
Ⅳ：Ⅲを反転したものです。Ⅱの元図とはあすび通し、踏み木の踏み順とも変化していますが、柄は同一です。

　元図は図4ですから、図1はまるで異なった柄のように見えます。

図4